Здравствуйте!
Сегодня, как я и обещал, мы рассмотрим угловые модули.
Это довольно простая тема, но у многих начинающих мебельщиков, она почему-то вызывает трудности.
И для примера, предлагаю разобрать проектировку самого обычного верхнего трапециевидного короба.
Конфигурация его может быть разной, в зависимости от назначения.
Он может быть рабочим (иметь внутри полки, или сушилку для посуды), а может быть и «обманкой», например, скрывать газовый котел, или колонку.
Итак, рассмотрим его вариант, когда внутри находятся полки.
Сам короб состоит из двух горизонтов, двух боков, двух полок и корпусной планки (фасад мы пока в расчет не берем, так как на это будет выделена отдельная тема). Да, еще у него будет две задних стенки из ДВП (для простоты, размеры ДВП (его толщину) мы в расчетах учитывать не будем).
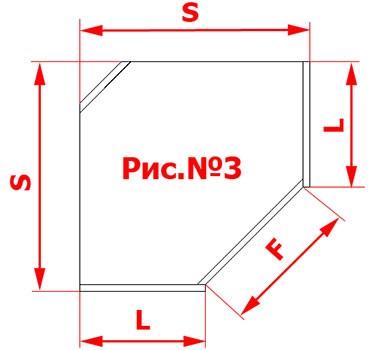
Он у нас будет симметричным, то есть его размеры по ширине и глубине S будут одинаковы, а соответственно и ширина боков L будет одна и та же (см. рис№3).
Самые важные расчеты подобных коробов, как правило, делаются «в плане», т.е. когда мы смотрим на него сверху.
Итак, рассматриваемый нами модуль можно спроектировать в двух вариантах:
В первом варианте считать нужно будет меньше, но он, будет иметь некоторые недостатки.
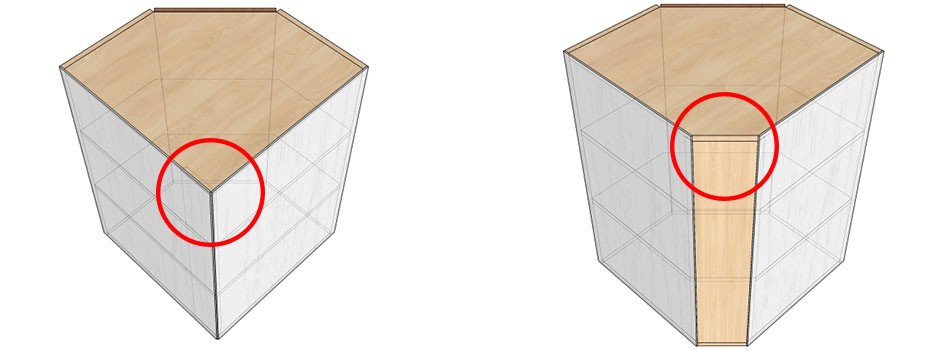
Эти недостатки будут заключаться в том, что при установке (навеске короба на стену в угол), могут возникнуть проблемы. И все это из-за прямого угла, который отмечен на рис.№1.
Во втором варианте (рис.№2), считать нужно немножко больше, но рассчитываемый короб будет иметь преимущество в установке.
Если угол, в который будет устанавливаться такой короб, будет иметь неровности, выпуклости и другие дефекты, все они останутся в свободном пространстве, образованном благодаря угловому срезу горизонтов и полок короба.
Давайте рассмотрим лучший (второй) вариант
Для начала, нужно определиться с габаритными размерами S.
От них напрямую будет зависеть ширина фасада, или, если для наглядности, размер F (рис.№3).
 Почему же нам так нужен это размер F?
Почему же нам так нужен это размер F?
На то есть свои причины.
Модуль иметь какую-то высоту H.
Так вот, чем больше будет размер F, тем больше геометрия фасада короба будет приближаться к квадрату (а он должен быть прямоугольником). А в этом случае, работа (открытие и закрытие) такого фасада, будет создавать большие нагрузки на петли, которыми он крепится ко всей конструкции. Разумеется, от этого они, работать лучше и дольше не станут.
Да и пользоваться таким фасадом будет не удобно, так как для его работы понадобится много свободного пространства.
 Но с другой стороны, если величина F будет небольшой (например, меньше 250 миллиметров), то короб получится не функциональным.
Но с другой стороны, если величина F будет небольшой (например, меньше 250 миллиметров), то короб получится не функциональным.
В проем фасада такой величины ничего нельзя будет положить.
Вот критерии, которые нужно учитывать в самом начале проектирования таких коробов.
Для ориентира, размеры угловых коробов (величина S), должны находятся в пределах от 500мм до 650 мм.
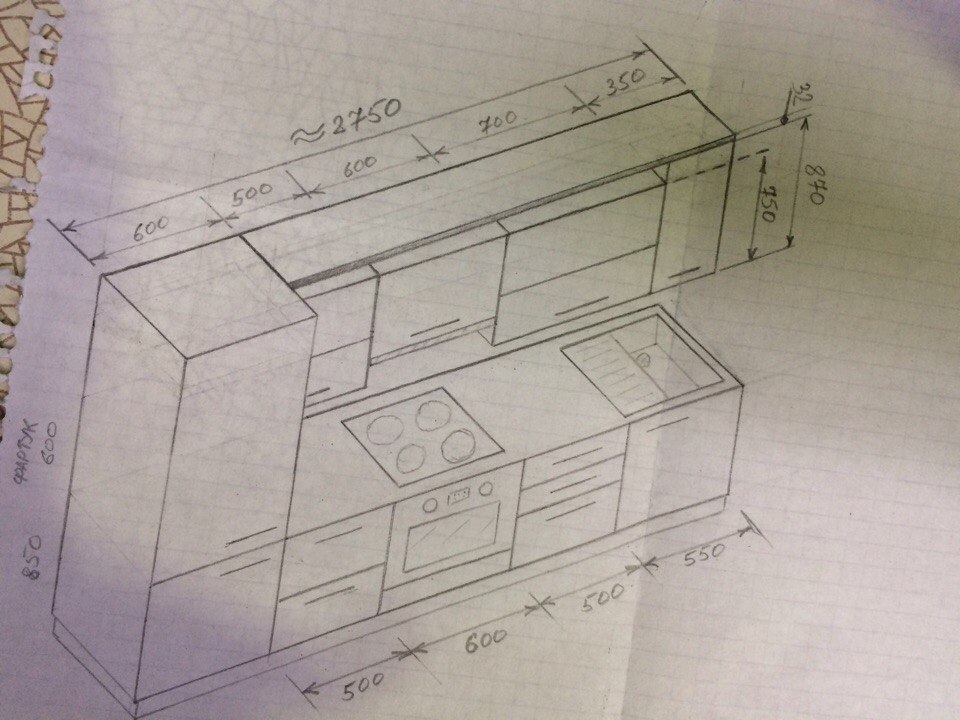
Пусть высота нашего короба будет 800 миллиметров. Давайте определимся с его габаритными глубиной и шириной (другими словами, с общими размерами).
Делать расчет можно двумя способами: от общих размеров S до размера F, и наоборот.
Но на практике, чаще всего используется первый вариант. Им мы и воспользуемся.
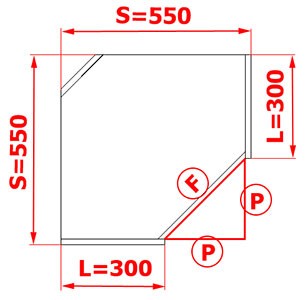
Предположим, что размеры короба (S) у нас будут 550 на 550 миллиметров, а ширина бока короба (L) будет равна 300 миллиметров. Высчитаем размер, под ширину фасада (F).
Сразу хочу оговориться, что в большинстве подобных случаев, нужно знать теорему Пифагора, которую изучают то-ли в 5-м, то-ли в 6-м классе средней школы.
Она очень проста, ее можно просто зазубрить (записать), и с расчетом подобных коробов проблем не будет.
А звучит эта теорема просто: Квадрат гипотенузы равен сумме квадратов катетов.
Или, если эту теорему перевести на наш пример, то прямоугольным треугольником у нас является треугольник FPP. Причем, он является не только прямоугольным, но еще и равнобедренным.
Для тех, кто не совсем понимает, что такое равнобедренный треугольник, скажу проще: у этого треугольника стороны P равны между собой (по той причине, что стороны короба S равны, так же, и ширина (глубина) боков L одинакова)
 Так как гипотенуза этого треугольника – это наш искомый размер F, а катеты P, значит можно записать следующее:
Так как гипотенуза этого треугольника – это наш искомый размер F, а катеты P, значит можно записать следующее:
F²=P²+P²=2P²
Упростив выражение, получим:
F=√‾2P² – эту формулу можно просто записать, и смело применять во всех случаях, которые соответствуют нашим условиям (а их два: размеры P короба равны, и ширина боков L то же одинакова). Кстати, эти условия соответствуют почти 99 процентам реально проектируемых угловых коробов.
Думаю, вы понимаете, что даже без знания математики, имея просто один калькулятор, можно делать расчеты угловых коробов.
Ну а сами расчеты начнем делать в следующей статье.
До встречи!







Спасибо, очень понятно, но не все. В этом примере чему равно Р в формуле для расчета фасада. Правильно ли я поняла, что Р = 550 – 16 -300 = 234 мм?
Совершенно верно. Вы даже забежали немножко вперед. О самих расчетах мы поговорим в следующем выпуске.
Вот если не ваш вопрос то долго ещё думать пришлось.
Спасибо, буду ждать следующих уроков
Спасибо,доступно и понятно.
ждём следующих уроков
Скажите пожалуйста, а если по проекту размеры L разные (например 450 и 350) не будет ли конструкция выглядеть кособоко и некрасиво? Спасибо.
Да, немного будет. Но бывают ситуации (довольно редко), когда так проектировать приходится.
спасибо надо попробовать.
Спасибо познавательно!
Спасибо за статью, расскажите пожалуйста про нахлест створок на каркас ДСП при угловом и прямоугоьном шкафу
Стас, вы могли бы детальнее изложить ваш вопрос?
спасибо супер
Петля не должно быть так устанавливать…..дверь не открывается на 90 градусов
Сюда устанавливается петля 45 градусов, которая специально рассчитана на такие модуля.
Спасибо за ответ, я новичок в этом деле….(I’m Sorry)
Немного не согласен с вашей формулой.Вы правильно сказали,что квадрат гипотенузы равен сумме квадратов катетов т.е F²=P²+P² далее F²=2P² и если взять корень с правой и левой части то получим F=√‾2 P ,не F=√‾2P².
Все верно, мы говорим об одном и том-же. F равно корню квадратному из 2P², или, как вы правильно заметили, корню квадратному из двойки, после чего это все умножается на P. Просто не смог найти в Word-е символ, который позволяет верхнюю черточку квадратного корня “протянуть” до конца выражения.
А почему внутрення полочка на 10 мм меньше основного габарита?
Потому, что при открытых фасадах, полки смотряться более эстетично (хотя это не принципиально).
Как повесить шкаф со скошенным углом?
Немного не понял вопрос, если можно – подробнее…
F получается будет 330 мм?
Если размер короба 550 на 550, а глубина бока 300, то F будет 353 мм.