Здравствуйте дорогие друзья.
В этой статье мы с вами рассмотрим угловой модуль, установленный на столешнице.
В данном случае, к этому модулю должен стыковаться (справа) пенал, содержащий духовой шкаф. Значит, чтобы не было проблем с установкой духовки (я имею в виду, его размер по глубине), сделаем глубину пенала немного с «запасом», то есть, 600мм.
В таком случае, бок углового короба (тот, который стыкуется с пеналом) должен быть так же глубиной 600мм.
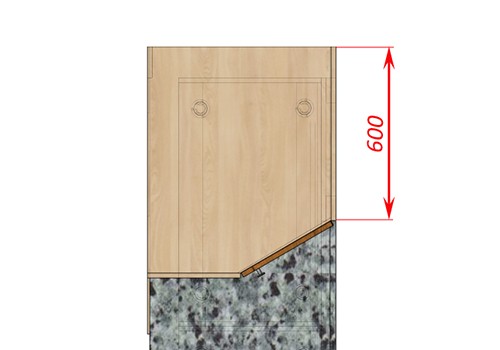Уже по этой причине, рассматриваемый нами модуль не может быть правильным многоугольником (помните, при проектировании углов, нужно стараться, чтобы в их основании лежали правильные многоугольники, так очень удобно их рассчитывать).
Итак, в нашем случае, нужно сделать следующее: Определить габариты короба таким образом, чтобы скос под фасад являлся гипотенузой треугольника со стандартными углами (30 и 60 градусов).
Это нужно для того, чтобы не было проблем с подборкой петель на фасады короба (петли на 30 и 60 градусов – стандартный вариант).
Итак, как пример, получился короб, ширина которой равна 608мм (ширина привязана к стыковочным планкам, и увеличении глубины столешницы, подробнее об этом написано в первой статье на эту тему), а глубина будет равна 745мм (как мы ее нашли – об этом написано ниже).
Соответственно, размеры горизонтов будут равны 592 – ширина, и 729 – глубина.
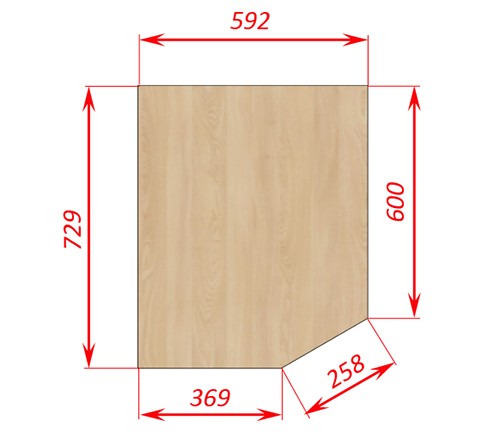Если сделать глубину верхних коробов, являющихся левым верхним крылом, и примыкающими к этому коробу, глубиной 369мм (например), то размер скоса под фасад получится равным 258мм (а сам фасад можно сделать шириной 256мм).
Кстати, как же рассчитать в данном случае такой горизонт?
А сделать это очень просто.
Определяемся сначала, какого размера нам нужен скос (в данном случае, исходя из рисунка, это составляющая (с) прямоугольного треугольника аbc).
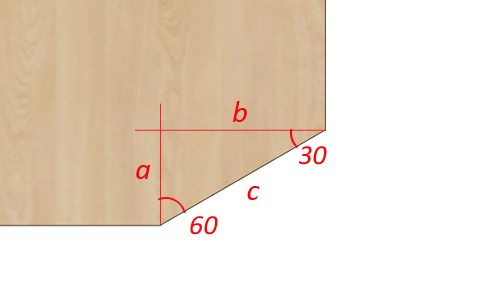Он у нас равен 258мм. То есть, с=258мм.
Теперь нам нужно всего лишь найти либо катет (а) или катет (b) этого прямоугольного треугольника.
А чтобы их найти, нужно выразить какую-либо их этих величин через тригонометрическую функцию с катетом (с), размер которого нам известен (258мм).
Например:
Sin30=1/2; а/с=1/2, то есть, а/258=1/2
Из этой пропорции находим (а).
Катет (а) получается равным 129мм.
Ну, а, зная размер (а) и зная размер одной из сторон горизонта (той, которая стыкуется с пеналом, и глубина которой равна 600мм), можем найти вторую сторону (противоположную):
600+129=729мм.
Зная две стороны прямоугольного треугольника ((а) и (с)), можем по теореме Пифагора найти третью сторону (b). Она получается равной 223мм.
Теперь, чтобы найти сторону горизонта (ту, которая будет определять глубину левого крыла верхних коробов), нужно сделать следующее:
592-223=369 (мм).
Вот так, в общем-то, не сложно, рассчитывается («в общих чертах», разумеется) верхний угловой короб, в основании которого лежит неправильный многоугольник.
А на этом я буду заканчивать, и прощаться с вами до следующего поста.
